方程思想
数学运算的大部分题型，都可以使用方程法思想来解答。其中，对于一些典型题型，如“盈亏问题”、“鸡兔同笼问题”、和差倍比问题“等等，使用方程法思想解题才是最快的。
一、基本方程
掌握基本的设元方法，准确找出题目中的等量关系进行列式，是数学运算中最重要的方法。
如何设x？
1.设小不设大(避免出现分数)
2.设中间量(方便列式)
3.求谁设谁(避免出现陷阱)
二、不定方程
除了基本方程外，在我们的解题过程中，经常会遇到含有 1 个未知数的方程，也可能遇到含有 2 个未知数 2 个方程的方程组，或者 3 个未知数 3 个方程的方程组，这些方程或者方程组一般都有确定的解。
解不定方程问题常用的解法：综合利用整数的奇偶性、自然数的质合性、数的整除特性、尾数法、余数特性、特殊值法、代入排除法等多种数学知识来得到答案。
三、不等式
在设元求解的过程中，根据题意所得方程可能是等式方程，也可能是不等式方程。即所求的值是一个数量区间，而非一个定值。相较于等式方程能求出精确值，不等式方程还需要我们对取值区间做出判断。
四、随笔练习
例1：（2018四川）甲车间的生产效率是乙车间的 1.5 倍，分别生产 1200 件相同的产品，甲车间所需时间比乙车间少 10 天。问甲、乙两个车间合作生产 3000 件相同的产品需要多少天？（ ）
A.20
B.25
C.30
D.35
解析
工作量 = 工作效率 × 工作时间，设甲车间的生产效率为 3x，乙车间的生产效率为 2x，由题意可知，1200÷2x-1200÷3x=10，解得 x=20。即甲车间每天生产 3×20=60 件，乙车间每天生产2×20=40 件。故题干所求为 3000÷（60+40）=30 天。故本题选 C。
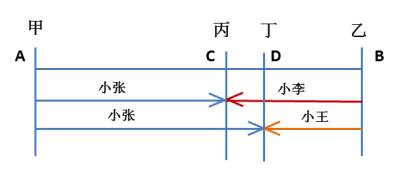
例2：（2019四川选调）小张从甲地出发匀速前往乙地，同时小李和小王从乙地出发匀速前往甲地，小张和小李在途中的丙地相遇，小张和小王在途中的丁地相遇。已知小张的速度比小李快一半，小王的速度比小李慢一半，则丙、丁两地之间的距离与甲、乙两地之间的距离之比为：（ ）
A. 2：15
B. 1：4
C. 3：20
D. 1：15
解析
路程 = 速度 × 时间，两人路程和(S) =速度和(V1+V2)× 相遇时间(T)。设甲乙两地的距离为s，小张、小李、小王的速度分别为、、3x、2x、x，由下图可知，小张和小李相遇时用时为t1=s÷(3x+2x)=s5x，小张和小王相遇时用时t2=s÷(3x+x)=s4x，则小张经过丙、丁两地路程用时t2−t1=s4x−s5x，所以丙、丁两地之间的路程丙丁（）S丙丁=3x×（s4x−s5x）=3s20，故题干所求为3s20:s=3:20。故本题选 C。
例3：（2019山东选调）某工厂生产过程中需要用到 A、B、C 三种零件，工厂仓库中原有三种零件的数量比为 1：2：3，现在采购部门新购进一批零件，新购进三种零件的数量比是 3：2：4，工厂每天使用的三种零件数量相同，当 A 零件用完的时候，B 零件还剩下 10 个，C 零件还剩下 170 个，请问工厂仓库中原有 A、B、C 零件各多少个？（ ）
A. 40，80，120
B. 50，100，150
C. 60，120，180
D. 70，140，210
解析
设原有三种零件的数量分别为 x、2x、3x，再次购买的数量分别为3y、2y、4y，由于每天使用的三种零件数量相同，所以 A、B、C 三种零件使用的总量相同。
（2x+2y）-（x+3y）=10 ①
（3x+4y）-（x+3y）=170 ②
解得 x=60，y=50。所以原有三种零件的数量分别为 60、120、180。选 C。
例4：（2009浙江）有271位游客欲乘大、小两种客车旅游，已知大客车有37个座位，小客车有20个座位。为保证每位乘客均有座位，且车上没有空座，则需大客车的辆数是：
A.1辆
B.3辆
C.2辆
D.4辆
解析
设大客车有x辆，小客车有y辆。根据题意可列方程：37x+20y=271。这是一个不定方程，20y的尾数一定是0，则37x的尾数必须是1，结合选项，只有x=3才满足条件。故正确答案为B。
例5：（2020广东）某部门正在准备会议材料，共有153份相同的文件，需要装到大小两种文件袋里送至会场，大的每个能装24份文件，小的每个能装15份文件。如果要使每个文件袋都正好装满，则需要大文件袋（ ）个。
A.2
B.3
C.5
D.7
解析
设需要大文件袋x个，小文件袋y个，由题意可列式为：24x+15y=153，化简可得8x+5y=51。这是一个不定方程，看到方程含5，利用倍数特性，5y的尾数0或5，51的尾数为1，推出8x的尾数6或1，又根据奇偶性，8x为偶数，因此8x的尾数为6，因此排除BC选项。
验证：x=7，8x=56，y=-1，排除，选A。
例6：（2019浙江15%）某地鼓励农户种植果树，规定每个自然年末种植果树面积比年初增加 5 亩，农民可得到 2000 元奖金，且超出 5 亩后每增加 1 亩可额外获得 x 元奖金。已知每个自然年种植的果树，从下一自然年起每亩每年可获得 y 元的果树收入。某农户第一年开始种植果树，当年种植 10 亩，获奖金 3500 元；第二年种植面积扩大 16 亩；第三年种植面积又扩大 15 亩，年收入比第一年的 16 倍多 1000 元。则以下哪个不等式能准确描述 x 与 y 的关系（ ）（注：年收入 = 奖金 + 果树收入）
A. x ＜ 0.2y
B. 0.2y ≤ x ＜ 0.5y
C. 0.5y ≤ x ＜ y
D. x ≥ y
解析
根据第一年的奖金情况可列式 3500-2000=5x，解得 x=300， 即超出5亩后每亩可额外获得 300元奖金。
第三年农民种植面积扩大15亩，增加5亩部分奖金依然为2000元，超出 15 - 5 = 10亩，额外奖金数 = 10x =3000元，此时第三年果树收入应该由第一年的果树10亩和第二年新增的果树16亩获得，则第三年果树收入 = （10 + 16）× y，所以第三年年收入 = 2000 + 3000 + 26y
根据题干条件第三年年收入比第一年的16倍还多1000元，得到等式：2000 + 3000 + 26y = 3500 x 16 + 1000，整理可得：5000 + 26y = 57000，解得 y=2000，综上可知：x = 300，y=2000；结合选项，只有A符合。