十字交叉
十字交叉法实际上是一种方程计算过程中的简化形式。主要用来解决两者之间的比例关系问题，在行测中资料分析以及数量关系都会涉及到。
一、十字交叉法
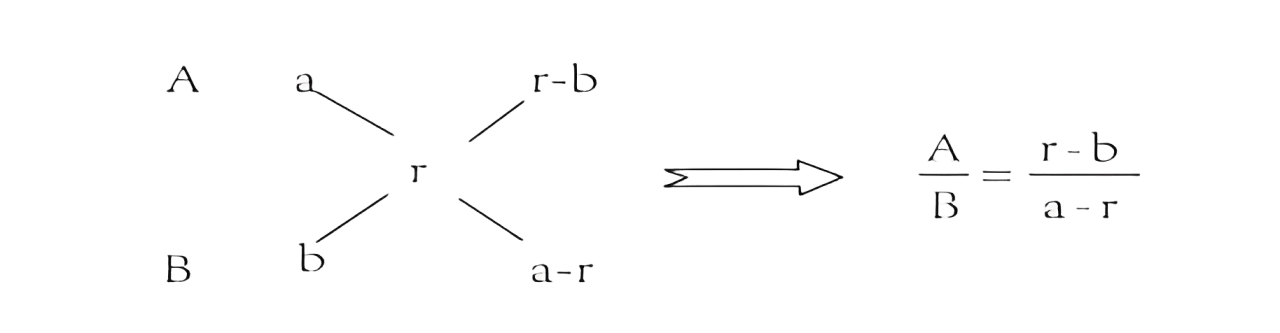
1、方法来源：十字交叉法最先是从溶液混合问题（两个部分混合成一个整体）衍生而来的。公式：浓度（%）=溶质溶液溶质溶液；若有两种溶液的质量分别为 A 与B ，其浓度分别为 a 与 b，混合后浓度为 r，则由溶质质量不变可列出下式 Aa+Bb=(A+B)r，对上式进行变形可得ab=r−ba−r，在解题过程中一般将此式转换成如下形式：
2、注意：一定要知道A与B代表的是什么。
3、口诀：整体写中间，部分写左边（大的在上，小的在下），交叉做差，得到分母之比。
二、适用题型
1、该方法一般适用于平均值的混合问题的题型，比如说：混合溶液、利润率、折扣、增长率、比重、平均数等，公式如下。
2、公式：：看到了符合以下的公式且存在混合的题目一般都能够运用十字交叉法。
浓度（%）=溶质溶液溶质溶液
利润率（%）=利润成本利润成本
折扣（%）=售价原价售价原价
比重（%）=部分整体部分整体
增长率（%）=增长量基期量增长量基期量
平均数=总数人数总数人数
比如：A班女生的比重为45%，B班女生的比重为60%，AB班女生的比重为55%。比重=女生/全班人数
利用口诀：A班人数/B班人数=5%/10%
三、线段法
线段法是十字交叉法的变形，只是换了一种画法而已
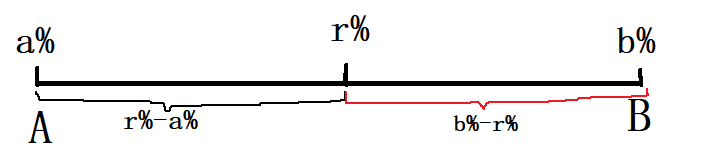
若有两种溶液的质量分别为 A 与B ，其浓度分别为 a 与 b，混合后浓度为 r，
口诀：
（1）部分写两边，整体写中间。
（2）距离和量成反比。（距离是指混合后的的距离和两端做差）
上面的图根据口诀可得：ab=r−ba−r
四、随笔练习
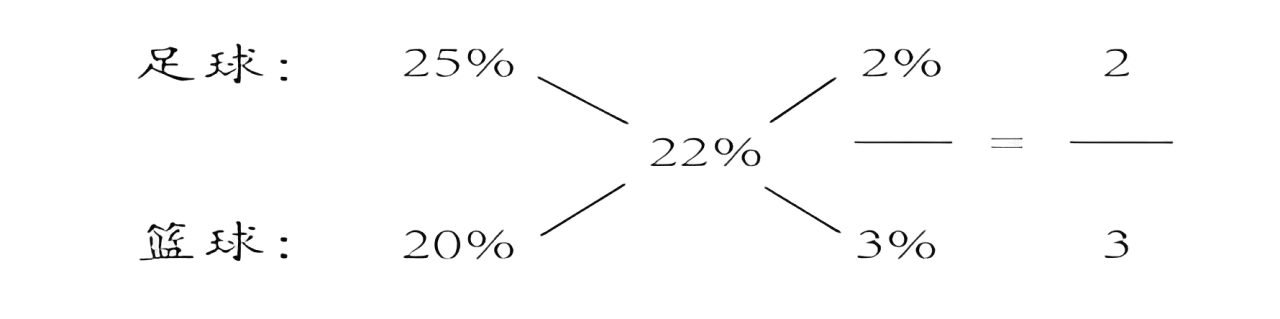
例1：（2014四川）学校体育部采购一批足球和篮球，足球和篮球的定价分别为每个 80 元和 100 元。由 于购买数量较多，商店分别给予足球 25%、篮球 20% 的折扣，结果共少付了 22%。问购买的足球和篮球的数量之比是多少？（ ）
A.4：5
B.5：6
C.6：5
D.5：4
解析
方法一：总折扣=折扣后总额/折扣前总额，足球部分少付了25%，篮球部分少付了20%，混合后少付了22%，典型 A，B 的混合题型，因此采用十字交叉法如下：
即足球价格总额与篮球价格总额之比为 2：3。注意该比例是足球折扣前总额和篮球折扣前总额的比，设足球共买了 x 个，篮球共买了 y 个，则可列式为 80x：100y=2：3，解得 x：y=5：6。故本题选 B
方法二：设足球共买了 a 个，篮球共买了 b 个，根据混合列式有25%×80a+20%×100b=（80a+100b）×22%，化简得60a+80b=62.4a+78b，因此a:b=5:6
例2：（2016联考）某高校艺术学院分音乐系和美术系两个系别，已知学院男生人数占人数的 30％，且音乐系男女生人数之比为 1：3，美术系男女生人数之比为 2：3，问音乐系和美术系的总人数之比为多少？
A.5：2
B.5：1
C.3：1
D.2：1
解析
音乐系男生人数占比=音乐系男生/音乐系总人数，美术系男生人数占比=美术系男生/美术系总人数，因为音乐系男女人数之比为 1：3，可得音乐系男生人数占比为1/4=25%，美术系男女人数之比为 2：3 可得美术系男生人数占比2/5=40%，混合后男生人数占人数的 30%，A，B 的混合题型，因此采用十字交叉法如下：
显然音乐系和美术系男生人数之比为 2：1，故本题选 D
例3：（2019江苏）某银行为一家小微企业提供了年利率分别为6％、7％的甲、乙两种贷款，期限均为一年。若两种货款的合计数额为400万元，企业需付利息总额为25万元，则乙种贷款的数额是：
A.100万元
B.120万元
C.130万元
D.150万元
解析
甲乙年利率分别为6％、7％，两种货款的合计数额为400万元，企业需付利息总额为25万元，则两种合计年利率为25400=6.25%，使用十字交叉，甲：乙=（7%-6.25%）:（6.25%-6%）=3：1 ，总共400万，乙占一份，则乙为100万元，所以答案为A
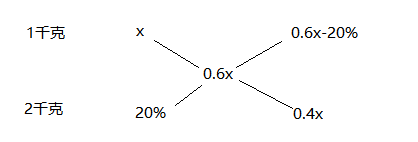
例4：（2016北京）将1千克浓度为X的酒精，与2千克浓度为20%的酒精混合后，浓度变为0.6X。则X的值为？
A.50% B.48
C.45% D.40%
解析
典型的溶液混合。
得到0.6X−0.20.4X=12。解得X=50%，选A
例5：（2017联考）甲乙两队举行智力抢答比赛，两队平均得分为92分，其中甲队平均得分为88分，乙队平均得分为94分，则甲乙两队人数之和可能是:
A.20 B.21
C.23 D.25
解析
平均数问题，甲队平均分=甲队总分甲队人数甲队总分甲队人数，乙队平均分=乙队总分乙队人数乙队总分乙队人数，混合后两队平均分=两队总分两队人数两队总分两队人数，因此采用十字交叉法，可得甲乙两队人数比=（94-92）：（92-88）= 2：4 = 1：2，那么甲：乙=1：2，则甲乙总人数为3的倍数，选B。