容斥问题​

一、两者容斥​

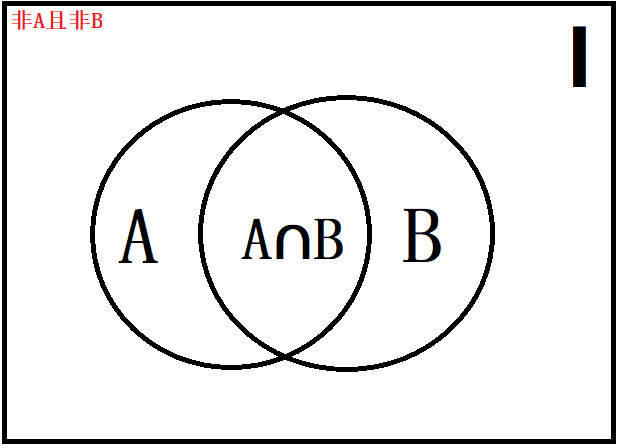
  如果被计数的事物有 A、B 两类，那么，先把 A、B 两个集合的元素个数相加，A 和 B 中都算了一次 A∩B 部分的元素，所以要把这部分重复计算的元素减去一次。如下图所示。

I-非A且非B=A+B-A‌∩B

如果题目中有提到类似“每人参加了至少一项”的表述，说明都不满足数=0、非A且非B=0

【记忆口诀】总数－都不 = 两集合之和 + 两集合之外数－两集合公共数

二、三者容斥​

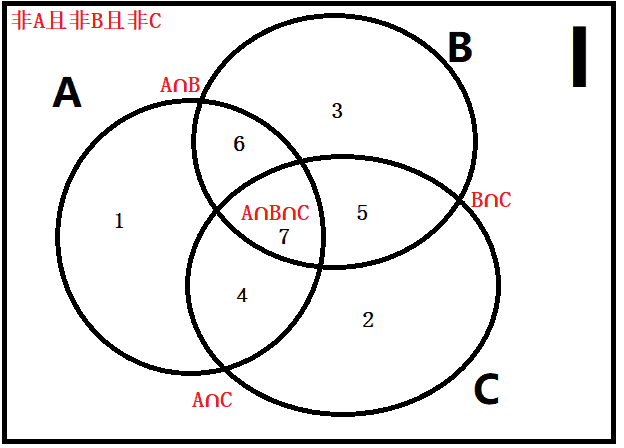
I-非A且非B且非C=A+B+C-A‌∩B-B‌∩C-A‌∩C+A‌∩B‌∩C

  三集合标准公式：总数－都不满足=A+B+C-(A∩B)-(A∩C)-(B∩C)+(A∩B∩C)
  三集合变形公式 ：总数－都不满足=A+B+C－只满足两项－2×满足三项

  如果题目中有提到类似“每人参加了至少一项”的表述，说明都不满足数=0，即 非A且非B且非C=0

解题步骤分三步走：

①画文氏图；

②弄清楚图形中每一部分所代表的含义；

③代入公式

三、容斥的极值问题​

方法1：多集合反向构造​

第一步：反向。先分别反向求出各集合的补集；例如：不喜欢音乐、舞蹈、美术的学生，分别有9、11、14人；

第二步：加和。反向的补集进行相加；例如：这9、11、14人毫无重复，则此时’不都喜欢’的最多，有9+11+14=34（人）；

第三步：做差。例如：’不都喜欢‘的最多，那么‘都喜欢的’最少，有45－34=11（人）。

这种思路的核心是“让不都喜欢的无任何重复，则不满足要求的最多”。

方法2：正向思路​

求最小值

两个集合A、B交集的最小值为A+B-U（U为全集）

三个集合A、B、C交集的最小值为A+B+C-2U（U为全集）

四个集合A、B、C、D交集的最小值为A+B+C+D-3U（U为全集）

求最大值

N个集合交集的最大值均为较小的集合

 

四、随笔练习​

例1：(2016年河南省) 某公司组织歌舞比赛，共 68 人参赛。其中，参加舞蹈比赛的有 12 人，参加歌唱比赛的有 18 人，45 人什么比赛都没有参加。问同时参加歌舞比赛的有多少人？ （ ）

A.7

B.8

C.9

D.10

※解析：总人数 = 参加舞蹈比赛人数 + 参加歌唱比赛人数 - 两项比赛都参加人数 + 两项比赛都未参加人数。所以两项比赛都参加的人数为 12+18-（68-45）=7 人。故答案为A

例2：(2011年国家) 某市对 52 种建筑防水卷材产品进行质量抽检，其中有 8 种产品的低温柔度不合格，10 种产品的可溶物含量不达标，9 种产品的接缝剪切性能不合格，同时两项不合格的有 7 种，有 1 种产品这三项都不合格。则三项全部合格的建筑防水卷材产品有多少种？ （ ）

A.34

B.35

C.36

D.37

※解析：在将低温柔度不合格、可溶物含量不达标、接缝剪切性能不合格的产品数相加时，两项同时不合格的产品数被计算了两次，需减掉一次；三项同时不合格的产品数被计算了三次，需减掉两次。设三项全合格的建筑防水卷材产品有 x 种，根据容斥原理可得，8+10+9-7-2×1+x=52，解得 x=34。故答案为A

例3：(2018年江西) 某高校做有关碎片化学习的问卷调查，问卷回收率为90%，在调查对象中有180人会利用网络课程进行学习，200人利用书本进行学习，100人利用移动设备进行碎片化学习，同时使用三种方式学习的有50人，同时使用两种学习方式的有20人，不存在三种学习都不用的人。那么这次共发放了多少份问卷？

A.370

B.380

C.390

D.400

※解析：这是一道三集合的容斥问题。注意题目中提到：不存在三种学习都不用的人。所以在套用三集合容斥问题非标准形式的过程中，非A且非B且非C=0。代入三集合容斥问题非标准形式得到：总人数=180+200+100-20-2*50，总人数=360，总问卷=360/90%=400。答案选D。

例4：(2024广东梅州事业单位) 某单位42名职工参加健身活动，每人至少参加一种，已知参加瑜伽的有22人，参加蛙跳的有30人，参加跑步的有15人，其中5名职工三种健身活动都参加了，该单位有（ ）名职工只参加了一种健身活动？

A.19

B.20

C.21

D.22

※解析：这是一道三集合的容斥问题。根据三集合容斥问题非标准型公式：A+B+C-满足两项-满足三项×2=总数-都不，可得：22+30+15-参加两种健身活动-5x2=42-0，解得参加两种健身活动的人数 = 15。根据三集合容斥问题常识公式：满足一项+ 满足两项 + 满足三项 = 总数-都不，则只参加一种健身活动的人数=42-15-5=22人。故正确答案为D。